FREQUENCY TABLES: PART II

Hopefully FREQUENCY TABLES: PART I is permanently emblazoned in your mind and heart. If not, here is the recap of the major points:

POINT #1: Frequency tables are all about summarizing COUNTS or the frequency with which something occurs, BUT NOT ALL NUMBERS IN A FREQUENCY TABLE REFER TO COUNTS! **Be sure you take the time to differentiate between numbers that represent COUNTS or FREQUENCIES and other numbers.

POINT #2: The column on the left is a list of VALUES that someone in the dataset provided. (They are NOT counts even if they are numbers).

POINT #3: FOCUS FIRST ON THE COUNT! Whatever you are doing with the frequency table, make sure you first recognize which column refers to the counts, and which columns do not. This is especially essential if the VALUES are also numerical. 

POINT#4: Interval/ratio variables are terrible candidates for frequency tables! This is especially true when they are continuous variables. (If you need a refresher on levels of measurement, click here). However, people can and commonly do make frequency tables by changing your variable (for example, to ordinal or nominal variables). 

POINT #5: Counts can tell you where the mode is, but counts are NEVER the mode. Students, repeat: COUNTS ARE NEVER THE MODE. They just tell you which category is the most frequent response, but the category itself is the mode. 

The mean and median can also be uncovered through frequency tables, but we have to expand them a little first. 

STEP 1 (VITAL!!): Determine your level of measurement. You may remember that NOMINAL VARIABLES DO NOT HAVE A MEAN OR A MEDIAN. 

	add, subtract, multiply, divide… (MEAN)	Greater than/less than (MEDIAN)	Difference (MODE)
Ratio	X	X	X
Interval	X (w/ caution)	X	X
Ordinal	-	X	X
Nominal	-	-	X

Because the mean requires addition and division, it only applies to ratio and interval variables. The median is the middle number when the values are arranged from lest to greatest, so it is only possible to compute it for ratio, interval and ordinal variable because nominal variables cannot be arranged from least to greatest. Mode applies to all levels of measurement because it is simply the most common response.

STEP 2: If you have a nominal variable, make the frequency table as shown in part I, find the most common category (the mode) and you are done!

If not, expand your table.

STEP 3: The first step in expanding the table is to find the cumulative frequency.

CUMULATIVE FREQUENCY=the total count up to a given point. Here is an example that builds on the GPA frequency table from PART I.

Picture #1

So, Column B hold the counts for each value, and Column C (our new column) holds the counts up to a certain point. Here it is crystal clear:

VERY LOW: There are 0 people in this category and it is the first category so it is everything up to that point.
VERY LOW through LOW: There are 3 people from "Very low" through "Low". From the beginning through the "Low" category, there are only 3 people (0 in "very low" plus 3 in "low").
VERY LOW through HIGH: There are 5 people from "very low" through "High". From the beginning through the "High" category, there are 5 people (0 in "very low" plus 3 in "low" plus 2 in "high").
VERY LOW through VERY HIGH: There are 10 people from "very low" through "very high". From the beginning through the "very high" category, there are 10 people (0 in "very low" plus 3 in "low" plus 2 in "high" plus 5 in "very high").

STEP 4: Add a new column, "cumulative percent". It is just like it sounds--the percent of people that the cumulative frequency represents.

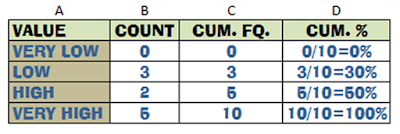Picture #2

The calculations appear in Column D, Cumulative Percent, but usually only the percentage appears. The calculation is a courtesy to make it more clear. Because there are 10 total observations (0+3+5+2=10, or just look at the biggest/last number in the Cumulative Frequency column) we divide each number in the Cumulative Frequency column (Column C) by the total (in this case 10).

This means that from the beginning through "very low" we have 0% of the total observations. From the beginning through "low" we have 30% of the total observations and so on. This is how we can find the median.

The median occurs at the 50% mark. (We call these "percent marks" percentiles). What is the median in Picture #2?

REMEMBER, THE MODE IS NEVER THE COUNT! THE COUNT TELLS YOU WHERE THE MODE IS, BUT IT IS NEVER THE MODE!

You don't have to pass it like this though...

Also, the 50% mark (50th percentile) after all the "HIGH" responses are accumulated, so we need to pass it! We do not PASS the 50% mark until the VERY HIGH category. BUT, the same rules apply here as in the past and because we have an even dataset, the median can technically be between two different values. Arrange them in order like you are familiar with and you will see:

LOW, LOW, LOW, HIGH, HIGH, VERY HIGH, VERY HIGH, VERY HIGH, VERY HIGH, VERY HIGH.

So our median here is between HIGH and VERY HIGH. And that's exactly how you report it with ordinal data: Between HIGH and VERY HIGH.

STORE IN LONG-TERM MEMORY: The same even numbered dataset rule applies to the median as before. If you see the exact 50th percentile in your frequency table, the median will be between the corresponding value and the next value. If it is an odd numbered set, you will not see the exact 50th percentile, and the median is in the category corresponding to the point where you have passed the 50th percentile.

Picture #3

Here is an odd numbered, similar version of the last dataset. What would the median be here?

Now the median is firmly within the "HIGH" category because that is the point where we have PASSED the 50th percentile.

STEP 5: Calculating the mean. Remember this figure of a frequency table of a ratio-level continuous variable (GPA)?

Picture #4

These are the kinds of frequency tables that are not very helpful. They are also the only kind for which you could calculate the mean. It is good practice to learn how to do it, and it may appear ON THE TEST in your stats class.

Let's go back to the "Slices of Pizza Eaten" frequency table from the last unit.

Picture #5

Here is the expanded table that also shows us how to compute the mean:

Picture #6

Again, focus on the COUNT! Look at the 1 slice of pizza row. The count is 4. So 4 people said that they ate one slice of pizza. Similarly, 1 person said they ate 2, 1 said they ate 3, 2 said they ate 4 and 2 said they ate 5. So we really have this:

1 1 1 1 2 3 4 4 5 5

You can see how you could simply add this to get: 1+1+1+1+2+3+4+4+5+5=27.

However, you could also make it easier by doing 4(1)+2+3+2(4)+2(5)=4+2+3+8+10=27.

Basically, the frequency table does the second. We simply multiple the value of each response by the count for that response. Then, we add up all of those multiplied values and divide by the total. Remember, the biggest value in the cumulative frequency column is the total number of observations. (Here the red arrow is pointing it out).


MAJOR TAKEAWAYS:

• Frequency tables can be expanded to include new columns: cumulative frequency (the total frequency up to a given point), and cumulative percent. (You could also add a category percentages column just be dividing the frequency of each response/category by the total number of observations--not discussed here).
• The level of measurement of the variable being used in the table determines the measures of central tendency that you can compute:
• Ratio/interval=mean, median, mode
• Ordinal=median, mode
• Nominal=mode only (discussed only in PART I)
• The median is the CATEGORY (not the COUNT) that corresponds to the point where you pass the 50th percent mark (percentile). If there is an exact 50th percent mark in the table, the media is right between that and the next category. 
• As in PART I, KEEP YOUR EYE ON THE COUNT!

FREQUENCY TABLES: PART I

A frequency table is a simple thing. Here is one:

PICTURE #1

...but BE CAREFUL it can be deceptively simple! It has trapped and deceived many statisticians over the years. You will be its next victim--or would have been except for this mini lesson. In just a few minutes, you will be Master of the Frequency Table.

A few keys to avoid deception:

POINT #1: Frequency tables are all about summarizing COUNTS or the frequency with which something occurs, BUT NOT ALL NUMBERS IN A FREQUENCY TABLE REFER TO COUNTS! **Be sure you take the time to differentiate between numbers that represent COUNTS or FREQUENCIES and other numbers.

Look at PICTURE #1 again. Which column of numbers are counts and which are not?

COUNT RECOGNITION

1. WHICH COLUMN IN PICTURE #1 ARE COUNTS?

The left
The right

ONLY the column on the RIGHT represents counts. So what are the numbers in the column on the left?

LEFT COLUMN CHECK

1. What do the numbers on the left in Picture #1 represent?

The number of times each person ate pizza
A total number of slices that was eaten by at least one person in the dataset
The number of people that ate pizza
A value of all theoretically possible numbers of slices that might be eaten by people
None of these

See how it can get tricky?

The column on the left is a number of pieces that at least one person ate. The column on the right is the NUMBER OF PEOPLE that ate that many pieces. MORE ON THIS LATER. For now just let it incubate as you move on to the next point.

POINT #2: The column on the left is a list of VALUES that someone in the dataset provided. It is clearer if we use values that are not numbers. Watch:

Picture #2

Now there is little (to no) confusion about which column contains the counts (frequencies) and which contains the values of the responses.

• 4 people said "bus" is their preferred mode of transportation
• 1 said "car (driving myself)"
• 1 said "car (getting a ride)"
• 2 said "skateboard"
• 3 said "bike"
• 5 said "walk" 
• and 1 said "other"

Easy to see. Now use the same eyes to look again at Picture #1:

Picture #1

How many people answered with each of the possible responses?

FIND THE COUNTS:

1. How many people answered with each of the possible responses?

1 person ate 4 slices, 2 ate 1, 3 ate 1, 4 ate 2 and 5 ate 2
4 people ate 1 slice, 1 ate 2, 1 ate 3, 2 ate 4 and 2 ate 5
1 slice ate 4 people, 2 slices ate 1 person, 3 slices ate 1 person, 4 ate 2 and 5 ate 2
None of these is correct
All are correct, in a sick way...

Not this count...

Starting to see it now? If not, here is tip #3 to master frequency tables:

POINT #3: FOCUS FIRST ON THE COUNT!

You simply will NOT fail if you focus first on the counts. In the first row of Picture #1, where is the COUNT? It is the column on the right. This is all a little facetious because it is labelled "Count". Don't worry, this is your chance to master the skill of "focusing on the COUNT". Surprisingly, this column often will be labeled either as "counts" or "frequency" or just and "f". Your job, first and foremost is to find that column. It is the absolute ground zero of the frequency table. That is why it is called a frequency table.

NOW YOU TRY>

Picture #3

Make a frequency table for the GPA data by filling in the worksheet below. Your grade will appear on the right.



If you figured that one out--A+ to you! If not, you are probably in really good company at this point. Why? Because frequency tables can be terribly tricky and deceptive as simple as they appear to be.

REMEMBER, FOCUS ON THE COUNT!

Not this count...

And the COUNT lives in Column B! Column A is just telling us all the values that were actual responses. And in this case, *THERE IS NO DUPLICATE VALUE* You notice this if you are focused on the count because you would have noticed that there is only 1 total COUNT of any given response!

In other words, everyone has a different GPA in this case, so there is one response for each value and each value gets its own row:

Here is the answer key. If you didn't get it, no sweat! This was a tough one--as long as you learned to focus on the COUNT, you came out with what you needed to learn!

Picture #4

This brings up the next point to avoid being tricked by frequency tables:

POINT#4: Interval/ratio variables are terrible candidates for frequency tables! This is especially true when they are continuous variables. (If you need a refresher on levels of measurement, click here). However, people can and commonly do make frequency tables by changing your variable. For example, what if we made this more of an ordinal variable by having just 4 categories instead of the exact GPA?

• 0-0.9999 (Let's call it "VERY LOW GPA")
• 1.0-1.9999 (Let's call it "LOW GPA")
• 2.0-2.9999 (Let's call it "HIGH GPA")
• 3.0-3.9999 (Let's call it "VERY HIGH GPA")

(Notice that the ".9999" endings make it so there is no overlap between categories. Otherwise even numbers would be included in both. E.g. 2.0 would be included in both "1.0-2.0" and "2.0-3.0" categories.)

Now let's look at the new table next to the old table (the colors illustrate the way we combined the categories):

Picture #5

Notice how we start to notice some trends now. For example, a lot of people have "very high" GPAs and no one has a "very low" GPA (grade inflation at work!). you may also notice that it tells a story about measures of central tendency (MEAN, MEDIAN and MODE). Let's quickly revisit those terms in a way that is so simple it almost doesn't do justice to them:

MEAN: All the numbers added up, divided by the total number of observations.
MEDIAN: The middle number when they are all sorted from smallest to largest (or the average of the two middle numbers if it there is an even number of observations).
MODE: The most common number.

You can find all three from this table! The MODE is the CATEGORY (>AHEM< THE "***!!!CATEGORY!!!***" )with the biggest COUNT. Keep your eye on the COUNT!

In this case, what is the mode in our new table with the new categories?

2
3
5
None of these is correct

KEEP YOUR EYE ON THE COUNT! If you answered 2 or 3 or 5, you were WRONG!! Why? Because THOSE ARE ALL COUNTS! Is the median GPA at a school the COUNT of some category? If you ask me the median GPA at Frantuckanilly State University and I told you 2,342 (the COUNT of people with an average GPA) would it make an sense to you?

POINT #5: A count (frequency) is NEVER the mean, median or mode!!

Read that sentence again 1,822 times. A count (frequency) is NEVER the mean, median or mode!

The count tells us where the mode is, but it is NOT the mode. Think of someone telling you the average GPA at their university is 9,286 and you will get the point.

So, in this case, what is the mode? Hopefully, if you got the mini quiz wrong you answered 5, because 5 is the count that indicates the mode--very high.

The mode is "very high" because it was the most frequent response.

you can also find out the mean and median, but to do this, we need to expand our frequency tables. You will learn how to do that in FREQUENCY TABLES: PART II. 

WHO IS REY?

If you saw Star Wars Episode 7 you may be wondering, Who is Rey? Rey herself said, "I am no one." Bu there is little doubt we will find out more about her past in the coming two movies. However, with release dates deep into the future, you may feel too anxious to wait! The Google search "Who is Rey?" Generates over 120 MILLION hits. The internet is ablaze with conversations and debates about what will be revealed in the next two movies.

If you are lucky enough to have some skills in statistics, you may be able to get ahead of the game. Remember that show "Who Wants to be a Millionaire?"? It was amazing that the poll the audience answers seemed to yield the correct response so often. Perhaps you could use statistics to "poll the audience" and it will give us the correct answer.

The problem is that with 129,000,000 matches and multiple possible theories being expressed on each matching web page, the task is formidable. Random sampling makes it possible to take a smaller number of those webpages and still end up with the same answer--at least it gives us a range that we are somewhat confident about (see other posts on sampling and confidence intervals on this cite).

First, it can be helpful to do some pre-research so that we have some idea what we are looking for. I have done it for us this time around and found nine theories (some related to others) and twelve criteria that people say should be satisfied by the theory.

The theories:

First, have a look at the nine theories:

• The Obi Wan's granddaughter theory (daughter of Luke and Obi Wan's daughter)
• The daughter of Luke Skywalker theory
• The daughter of Luke and a "Mara Jade" type Jedi theory
• The daughter of Luke and a "Mara Jade"-turned-evil theory
• The daughter of Leia and Han Solo theory
• The daughter of Leia-turned-evil and Han Solo theory
• The daughter of Obi Wan Kanobi theory
• The conceived by the force theory
• The reincarnated Anakin Skywalker ("Chosen one") theory

These were gathered by a purposive selection of articles that seemed most relevant. Purposive sampling means that articles are chosen based on the information they can provide. The results of purposive samples are not generalizable (able to be applied to the whole population) but can be an excellent choice in exploratory research or in pre-research because it helps the researcher get their bearing with major themes relevant to the study. In this case, it helped us uncover nine theories that we kept hearing over and over again.

There could be millions of potential theories, but we can know when to stop doing our pre-research when we start hearing only the same major theories over and over again. (We sometimes call this saturation).

The criteria:

Next, there were also twelve criteria that people kept talking about. According to the articles and comments read, these are things that the theory should satisfy for the theory to be chosen by those making the movie. A good theory should:

• Have the ability to explain Rey's advanced abilities with the force
• To explain her advanced pilot skills
• To explain her advanced mechanical skills
• To explain why she was abandoned (or placed) on Jakku as a young child
• To explain Maz Kanata's statement that Rey's family is not coming back
• To explain the draw Rey has to Luke's/Anakin's lightsaber
• Keep the movies Skywalker family-centric (to meet a statement made by creators of the movies)
• Create an interesting plot twist
• Be true to the Star Wars feel (and perhaps parts of even the expanded universe EU)
• Explain Obi Wan's "first steps" line in Rey's vision
• Explain cinematographic allusions or foreshadowing about who Rey is (like the look of her clothing or her upbringing on a dust planet).
• Explain the apparent connection between Rey and Leia toward the end of the movie

There are two ways to look at the "worthiness" of a theory vis-a-vis the criteria: How well a theory meets each criterion, and how many of the criteria it meets. One theory may provide a fascinating and excellent explanation about Rey's ability as a pilot but completely fail to explain Rey hearing Obi Wan's voice during her vision. Similarly, one theory may provide a fair explanation of all these criteria, but another may provide phenomenal explanations for half of the criteria. 

This will have to be sorted out later. But, just keep in mind that our evaluation of these theories will be some combination of how good the theory is at explaining each criterion, and how many of the criteria the theory explains. These could be called "depth" and "breadth" respectively. 

Preliminary results

There are many possible ways to go about this but one is to make a crosstabulation (crosstab). This simply means that we put the categories of one thing as column headers, and the categories of the other as row headers, and they we will in the frequencies we observe at the intersection. (In practice we usually make two variables and the "intersect" or "cross" them using statistics software). 

For now, I have filled in each cell with my subjective analysis based on my readings. 

The table is below:

This is simply the product of me rating each theory (in rows ->) as + , ++ , or +++ where + means "the theory would provide a decent explanation" and +++ means "the theory would provide a very good explanation". Notice there is also a - rating, meaning "this would provide a bad explanation of the criterion".

Now, back to the two ways of assessing the results: depth and breadth. If you scroll over to the right, you can see the total number of points each theory got. This is its overall strength and is simply the total number of + that it has, minus the total number of -. So + gets 1 point, ++ gets 2 points, +++ gets 3 points and - gets -1 point.

To the right of that is another column that give each theory a point for each criterion that it satisfies with at least one + .

Results

Rank by total points (depth):

1. Reincarnated Anakin/Chosen one
2. Daughter of Luke and "Mara Jade"-turned-evil
3. Daughter of Han Solo and Leia-turned-evil
4. Daughter of Luke and "Mara Jade"
5. Luke's daughter
6. Force conceived
7. Daughter of Luke and the daughter of Obi Wan's
8. Daughter of Han Solo and Leia
9. Daughter of Obi Wan

As we see here, the more simple versions of theories are less able to provide strong explanations for the different criteria on average. The top theories involve more details and usually, a woman that has turned evil. The internet world tends to find some appeal in the idea that there will be a "Rey, I am your mother" moment over the next two movies at some point. The idea is that either "Mara Jade"/Luke's Jedi wife turned evil in a sort of Darth Sidius reversal. She feels that the only way to conquer the dark side is to make one's way into it and then destroy it from within. Luke, disagreeing with this philosophy parts ways with his wife and has to hide their young daughter (Rey) and wipe her memory. Nevertheless, she has some Jedi training from Luke (and possibly ghost Obi Wan) that resurfaces later on, making Rey as powerful as we see in the movie. So, Luke's estranged wife will turn out to be either Snoke (a disguise) or Phasma, and, upon learning of Rey, try to bring her to the dark side. Some in this camp even think it may be Ben's intention to do the same, thus the scene where he looks at the Darth Vadar mask and says, "I will finish what you started"--not referring to destroying all Jedi, but to restoring balance to the force by passing through the dark side. 

A similar vibe runs through the Leia-turned-evil theory--that she is not pleased with the inability of the republic to put down the first order and decides to take a small band of resistance fighters to do it. Thus, the resistance is portrayed as a small movement with rudimentary spacecraft rather than more elaborate ships and equipment. This could play out with some similar "Rey, I am your mother" moments, and many believe that Leia might also be behind Snoke (as a disguise). Other possibilities behind Leia's turn to the dark side might be related to her inability to face the darkside like Luke did with Darth Vadar, her lack of training in the force by the light side, or, possibly the same thing that would turn a "Mara Jade" character to the dark side--fighting it from within. 

The #1 theory, however, does not have this tone. Instead, it portrays Rey as a reincarnation of Anakin, or the Chosen one. In this theory, the "Chosen one" is not a single person, but takes on many different personas over time through reincarnation. Thus, Rey is, in a sense, Anakin, out to undo the mistakes of his past life. We see Rey on a dusty run-down planet, good at flying and fixing things, and some argue that Rey bears a remarkable resemblance to Shmi Skywalker. This theory obviously explains a lot of criteria because it is sort of the catch-all--instead of answering how she is related to Anakin (a point that seems to be pretty overtly made by the movie makers), it simply asserts that she is him. However, this theory provides great depth of explanations for a lot of the criteria, but not as much breadth as others. For example, it does not offer a ready explanation of why she was abandoned as a young child or hears Obi Wan Kenobi's voice in her vision. 

Let us look at the ranking by breadth--percent of criteria satisfied:

1. Daughter of now-evil "Mara Jade" and Luke
2. (tie for 1st) Daughter of Han and now-evil Leia
3. Reincarnated chosen one 
4. Daughter of "Mara Jade" and Luke
5. (tie for 4th) Luke's daughter
6. Daughter of Obi Wan's daughter and Luke
7. (tie for 6th) Obi Wan's daughter
8. Daughter of Leia and Han
9. Force conceived

Once again, there is the general trend that more complex theories involving women turned evil are at the top! In fact, the same theories occupy the top three places, but the "reincarnated chosen one"theory has fallen to 3rd. This is because, while it satisfies many of the criteria very well, it does not satisfy as many of the criteria as some other theories.

Conclusion

Short of drawing up and conducting a full survey to a representative sample of the Star Wars fan universe, we conclude that three of the theories seem to land at the top:

1. Daughter of now-evil "Mara Jade" and Luke
2. Daughter of Han and now-evil Leia
3. Reincarnated chosen one 

So, which should be crowned the best? Here, we might want to weight depth or or breadth differently--implying that one is more important than the other. But, assuming we weight them equally, we just average them and end up with these final standings:

1. Daughter of now-evil "Mara Jade" and Luke
2. Daughter of Han and now-evil Leia
3. (tie for 2nd) Reincarnated chosen one 

So, in episode 8 when most of the world finds out that Rey is the daughter of Luke and a "Mara Jade" type Jedi-turned Phasma who was trained by Luke and ghost Obi Wan but had her memory wiped and was sent to Jakku to protect her from the dark side and her mother, maybe you will be able to say you heard it here first thanks to the power of analysis.