FREQUENCY TABLES: PART II

Hopefully FREQUENCY TABLES: PART I is permanently emblazoned in your mind and heart. If not, here is the recap of the major points:

POINT #1: Frequency tables are all about summarizing COUNTS or the frequency with which something occurs, BUT NOT ALL NUMBERS IN A FREQUENCY TABLE REFER TO COUNTS! **Be sure you take the time to differentiate between numbers that represent COUNTS or FREQUENCIES and other numbers.

POINT #2: The column on the left is a list of VALUES that someone in the dataset provided. (They are NOT counts even if they are numbers).

POINT #3: FOCUS FIRST ON THE COUNT! Whatever you are doing with the frequency table, make sure you first recognize which column refers to the counts, and which columns do not. This is especially essential if the VALUES are also numerical. 

POINT#4: Interval/ratio variables are terrible candidates for frequency tables! This is especially true when they are continuous variables. (If you need a refresher on levels of measurement, click here). However, people can and commonly do make frequency tables by changing your variable (for example, to ordinal or nominal variables). 

POINT #5: Counts can tell you where the mode is, but counts are NEVER the mode. Students, repeat: COUNTS ARE NEVER THE MODE. They just tell you which category is the most frequent response, but the category itself is the mode. 

The mean and median can also be uncovered through frequency tables, but we have to expand them a little first. 

STEP 1 (VITAL!!): Determine your level of measurement. You may remember that NOMINAL VARIABLES DO NOT HAVE A MEAN OR A MEDIAN. 

	add, subtract, multiply, divide… (MEAN)	Greater than/less than (MEDIAN)	Difference (MODE)
Ratio	X	X	X
Interval	X (w/ caution)	X	X
Ordinal	-	X	X
Nominal	-	-	X

Because the mean requires addition and division, it only applies to ratio and interval variables. The median is the middle number when the values are arranged from lest to greatest, so it is only possible to compute it for ratio, interval and ordinal variable because nominal variables cannot be arranged from least to greatest. Mode applies to all levels of measurement because it is simply the most common response.

STEP 2: If you have a nominal variable, make the frequency table as shown in part I, find the most common category (the mode) and you are done!

If not, expand your table.

STEP 3: The first step in expanding the table is to find the cumulative frequency.

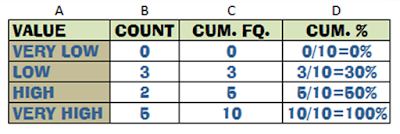
CUMULATIVE FREQUENCY=the total count up to a given point. Here is an example that builds on the GPA frequency table from PART I.

Picture #1

So, Column B hold the counts for each value, and Column C (our new column) holds the counts up to a certain point. Here it is crystal clear:

VERY LOW: There are 0 people in this category and it is the first category so it is everything up to that point.
VERY LOW through LOW: There are 3 people from "Very low" through "Low". From the beginning through the "Low" category, there are only 3 people (0 in "very low" plus 3 in "low").
VERY LOW through HIGH: There are 5 people from "very low" through "High". From the beginning through the "High" category, there are 5 people (0 in "very low" plus 3 in "low" plus 2 in "high").
VERY LOW through VERY HIGH: There are 10 people from "very low" through "very high". From the beginning through the "very high" category, there are 10 people (0 in "very low" plus 3 in "low" plus 2 in "high" plus 5 in "very high").

STEP 4: Add a new column, "cumulative percent". It is just like it sounds--the percent of people that the cumulative frequency represents.

Picture #2

The calculations appear in Column D, Cumulative Percent, but usually only the percentage appears. The calculation is a courtesy to make it more clear. Because there are 10 total observations (0+3+5+2=10, or just look at the biggest/last number in the Cumulative Frequency column) we divide each number in the Cumulative Frequency column (Column C) by the total (in this case 10).

This means that from the beginning through "very low" we have 0% of the total observations. From the beginning through "low" we have 30% of the total observations and so on. This is how we can find the median.

The median occurs at the 50% mark. (We call these "percent marks" percentiles). What is the median in Picture #2?

REMEMBER, THE MODE IS NEVER THE COUNT! THE COUNT TELLS YOU WHERE THE MODE IS, BUT IT IS NEVER THE MODE!

You don't have to pass it like this though...

Also, the 50% mark (50th percentile) after all the "HIGH" responses are accumulated, so we need to pass it! We do not PASS the 50% mark until the VERY HIGH category. BUT, the same rules apply here as in the past and because we have an even dataset, the median can technically be between two different values. Arrange them in order like you are familiar with and you will see:

LOW, LOW, LOW, HIGH, HIGH, VERY HIGH, VERY HIGH, VERY HIGH, VERY HIGH, VERY HIGH.

So our median here is between HIGH and VERY HIGH. And that's exactly how you report it with ordinal data: Between HIGH and VERY HIGH.

STORE IN LONG-TERM MEMORY: The same even numbered dataset rule applies to the median as before. If you see the exact 50th percentile in your frequency table, the median will be between the corresponding value and the next value. If it is an odd numbered set, you will not see the exact 50th percentile, and the median is in the category corresponding to the point where you have passed the 50th percentile.

Picture #3

Here is an odd numbered, similar version of the last dataset. What would the median be here?

Now the median is firmly within the "HIGH" category because that is the point where we have PASSED the 50th percentile.

STEP 5: Calculating the mean. Remember this figure of a frequency table of a ratio-level continuous variable (GPA)?

Picture #4

These are the kinds of frequency tables that are not very helpful. They are also the only kind for which you could calculate the mean. It is good practice to learn how to do it, and it may appear ON THE TEST in your stats class.

Let's go back to the "Slices of Pizza Eaten" frequency table from the last unit.

Picture #5

Here is the expanded table that also shows us how to compute the mean:

Picture #6

Again, focus on the COUNT! Look at the 1 slice of pizza row. The count is 4. So 4 people said that they ate one slice of pizza. Similarly, 1 person said they ate 2, 1 said they ate 3, 2 said they ate 4 and 2 said they ate 5. So we really have this:

1 1 1 1 2 3 4 4 5 5

You can see how you could simply add this to get: 1+1+1+1+2+3+4+4+5+5=27.

However, you could also make it easier by doing 4(1)+2+3+2(4)+2(5)=4+2+3+8+10=27.

Basically, the frequency table does the second. We simply multiple the value of each response by the count for that response. Then, we add up all of those multiplied values and divide by the total. Remember, the biggest value in the cumulative frequency column is the total number of observations. (Here the red arrow is pointing it out).


MAJOR TAKEAWAYS:

• Frequency tables can be expanded to include new columns: cumulative frequency (the total frequency up to a given point), and cumulative percent. (You could also add a category percentages column just be dividing the frequency of each response/category by the total number of observations--not discussed here).
• The level of measurement of the variable being used in the table determines the measures of central tendency that you can compute:
• Ratio/interval=mean, median, mode
• Ordinal=median, mode
• Nominal=mode only (discussed only in PART I)
• The median is the CATEGORY (not the COUNT) that corresponds to the point where you pass the 50th percent mark (percentile). If there is an exact 50th percent mark in the table, the media is right between that and the next category. 
• As in PART I, KEEP YOUR EYE ON THE COUNT!